how to find a in vertex form

Follow this blog and be one step ahead.

Vertex form of Quadratic Functions is

$y=a(x-p)^2+q$

where

$a \neq 0$

It can give us lots of information about the quadratic function like location of vertex, domain, range, axis of symmetry, minimum or maximum value etc. In this article if you stay with me you can easily learn how to find all these variables.

Vertex:Location of vertex is (p, q) for function

$y=(x-p)^2+q$

. If our function is

$y=2(x-2)^2+3$

then its vertex would be located at (2, 3). If our function is

$y=2(x+5)^2-2$

then its vertex would be located at (-5, -2). If our function is

$y=-2(x+5)^2+2$

then its vertex would be located at (-5, 2).

Note that

$y=2(x+5)^2-2$

can be written as

$y=2(x-(-5))^2-2$

to find value of p and q when we compare it with

$y=a(x-p)^2+q$

Direction of Opening:Direction of opening of graph is upwards if

$a>0$

. If,

$a<0$

then direction of opening of graph would be downwards. Example, direction of opening of

$y=2(x-(-5))^2-2$

would be upwards. Direction of opening of

$y=-2(x+5)^2+2$

would be downwards. Visit Learn direction of opening of quadratic functions by sketching.

Minimum or Maximum Value: When graph of function is going upwards then we have minimum value which is y=q. If direction of opening is downwards then we have maximum value which is also y=q. For quadratic function

$y=(x-2)^2+4$

which is opening upwards we will have minimum value which would be

$y=q$

i.e

$y=4$

. For quadratic function

$y=-(x+2)^2-4$

which is opening downwards we will have maximum value. Our maximum value would be

$y=q$

which is

$y=-4$

Axis of Symmetry:Axis of symmetry is a straight vertical line which divides graph of quadratic function into two equal parts. It passes through the vertex of the graph. Equation of axis of symmetry is always equal to

$x=p$

. If we have quadratic function

$y=2(x-2)^2+3$

then by comparing it with

$y=(x-p)^2+q$

, we have

$p=2$

. Therefore, equation of axis of symmetry is

$x=2$

. If we have quadratic function

$y=-4(x+4)^2-8$

then by comparing it with

$y=(x-p)^2+q$

, we have

$p=-4$

. Therefore, equation of axis of symmetry is

$x=-4$

. For function

$y=(x-2)^2+2$

, equation of axis of symmetry would be

$x=2$

which shows in picture c.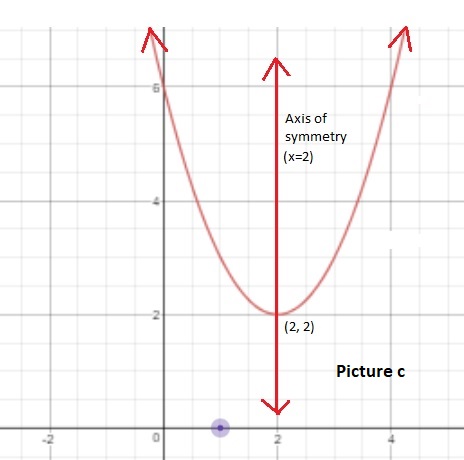

Domain:Domain is the collection of all

$x$

values present on the graph of quadratic function. In most of the cases, domain of the quadratic function would be all real numbers which can be written as {

$x|x \in R$

}. There are different notations to represent this. One of the notation can be written like (

$-\infty, \infty$

). But in some cases our domain can be different. For example, we have vertex function

$y=2(x-2)^2+3$

and If I hypothetically say that y is the distance covered in meters and

$x$

is the time taken in seconds. Domain here cannot be all real numbers because time cannot be in negative. Domain in this case would be {

$x|x \geq 0$

}. For function

$y=(x-2)^2+2$

, its graph is drawn above in picture c. Domain here is all real numbers. As graph moves upwards, it covers all the negative values in -x direction and all the positive values in the +x direction.

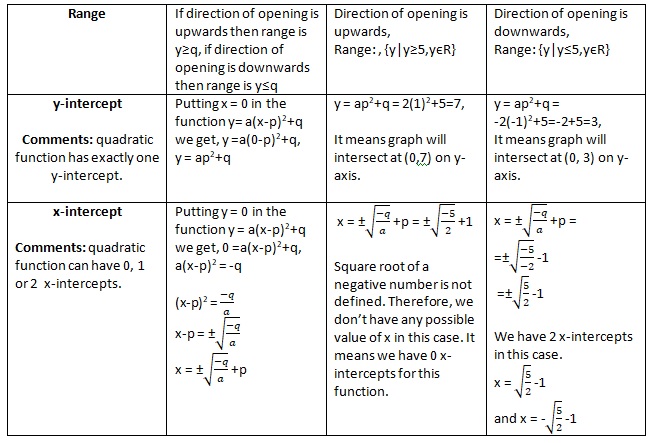
Range: Range is the collection of all

$y$

values present on the graph of quadratic function. Range depends on two separate cases.

If our graph is going downwards then we have maximum value. Our range in this case would be {

$y| y \leq q, y \in R$

If our graph is going upwards then we have minimum value. Our range in this case would be {

$y| y \geq q, y \in R$

}. For function

$y=(x-2)^2+2$

we have graph drawn above in picture c. Range in this case would be {

$y| y \geq 2,y \in R$

}. You can note that

$y$

value of the graph is minimum at

$y=2$

. We don't have y value less than 2 but all the y values are greater than or equal to 2.

y-intercept: y-intercept is the point where graph meets y-axis. Quadratic function has exactly one y-intercept.

To find y-intercept we put x =0 in the function

$y=a(x-p)^2+q$

we get

$y=a(0-p)^2+q$

$\Rightarrow y=ap^2+q$

Example, we have quadratic function

$y=-2(x-2)^2+3$

y-intercept for this function

$= ap^2+q=-2(2)^2+3=-8+3=-5$

It means that graph is going to intersect at point (0,-5) on y-axis.

x-intercept: x-intercept is the point where graph meets x-axis. Quadratic function can have 0,1 or 2 x-intercepts.

To find x-intercept we put y =0 in the function

$y=a(x-p)^2+q$

we get

$0=a(x-p)^2+q$

$\Rightarrow -q=a(x-p)^2$

$\Rightarrow \frac{-q}{a}=(x-p)^2$

$\Rightarrow \pm \sqrt\frac{-q}{a}=x-p$

$\Rightarrow \pm \sqrt\frac{-q}{a}+p=x$

$\Rightarrow x=\pm \sqrt\frac{-q}{a}+p$

how to find a in vertex form

Source: https://mathinstructor.net/2018/10/quadratic-functions-in-vertex-form-how-to-find-vertex-domain-range-axis-of-symmetry-minimum-or-maximum-direction-of-opening-x-intercept-y-intercept/

Posted by: bainknoted.blogspot.com