Let F(X) = Cxk Be A Power Function Such That F(4) Is 14 Times The Size Of F(1). What Is The Power K?

Polynomial and Rational Functions

Ability Functions and Polynomial Functions

Learning Objectives

In this section, yous will:

Place ability functions.
Identify end behavior of power functions.
Identify polynomial functions.
Identify the caste and leading coefficient of polynomial functions.

Three birds on a cliff with the sun rising in the background. — **Figure ane.** (credit: Jason Bay, Flickr)

Suppose a sure species of bird thrives on a small island. Its population over the last few years is shown in (Figure).

Year	$2009$	$2010$	$2011$	$2012$	$2013$
Bird Population	$800$	$897$	$992$	$1,083$	$1,169$

The population can exist estimated using the function $\,P\left(t\right)=-0.3{t}^{3}+97t+800,\,$ where $\,P\left(t\right)\,$ represents the bird population on the island $\,t\,$ years subsequently 2009. We can use this model to guess the maximum bird population and when it will occur. Nosotros can also employ this model to predict when the bird population volition disappear from the island. In this section, we will examine functions that we can use to gauge and predict these types of changes.

Identifying Power Functions

Before we can understand the bird problem, it volition be helpful to sympathize a unlike type of function. A power part is a function with a single term that is the production of a real number, a coefficient, and a variable raised to a fixed existent number.

As an instance, consider functions for area or volume. The part for the area of a circumvolve with radius $\,r\,$
is

$A\left(r\right)=\pi {r}^{2}$

and the role for the volume of a sphere with radius $\,r\,$
is

$V\left(r\right)=\frac{4}{3}\pi {r}^{3}$

Both of these are examples of power functions considering they consist of a coefficient, $\,\pi \,$ or $\,\frac{4}{3}\pi ,\,$ multiplied by a variable $\,r\,$ raised to a power.

Power Function

A ability part is a function that can be represented in the form

$f\left(x\right)=k{x}^{p}$

where $\,k\,$
and $\,p\,$ are real numbers, and $\,k\,$
is known as the coefficient.

Is $\,f\left(x\right)={2}^{x}\,$ a power function?

No. A power function contains a variable base raised to a fixed power. This function has a constant base raised to a variable ability. This is called an exponential function, not a power office.

Identifying Power Functions

Which of the following functions are power functions?

$\begin{array}{cccc}\hfill f\left(x\right)& =& 1\hfill & \phantom{\rule{2em}{0ex}}\text{Constant function}\hfill \\ \hfill f\left(x\right)& =& x\hfill & \phantom{\rule{2em}{0ex}}\text{Identify function}\hfill \\ \hfill f\left(x\right)& =& {x}^{2}\hfill & \phantom{\rule{2em}{0ex}}\text{Quadratic function}\hfill \\ \hfill f\left(x\right)& =& {x}^{3}\hfill & \phantom{\rule{2em}{0ex}}\text{Cubic function}\hfill \\ \hfill f\left(x\right)& =& \frac{1}{x}\hfill & \phantom{\rule{2em}{0ex}}\text{Reciprocal function}\hfill \\ \hfill f\left(x\right)& =& \frac{1}{{x}^{2}}\hfill & \phantom{\rule{2em}{0ex}}\text{Reciprocal squared function}\hfill \\ \hfill f\left(x\right)& =& \sqrt{x}\hfill & \phantom{\rule{2em}{0ex}}\text{Square root function}\hfill \\ \hfill f\left(x\right)& =& \sqrt[3]{x}\hfill & \phantom{\rule{2em}{0ex}}\text{Cube root function}\hfill \end{array}$

[reveal-answer q="fs-id1165137422823″]Bear witness Solution[/reveal-answer]
[hidden-reply a="fs-id1165137422823″]

All of the listed functions are power functions.

The constant and identity functions are power functions because they can be written every bit $\,f\left(x\right)={x}^{0}\,$ and $\,f\left(x\right)={x}^{1}\,$ respectively.

The quadratic and cubic functions are power functions with whole number powers $\,f\left(x\right)={x}^{2}\,$ and $\,f\left(x\right)={x}^{3}.$

The reciprocal and reciprocal squared functions are power functions with negative whole number powers considering they can exist written every bit $\,f\left(x\right)={x}^{-1}\,$ and $\,f\left(x\right)={x}^{-2}.$

The square and cube root functions are ability functions with fractional powers because they tin can be written as $\,f\left(x\right)={x}^{\frac{1}{2}}\,$ or $\,f\left(x\right)={x}^{\frac{1}{3}}.$

[/subconscious-answer]

Endeavor It

Which functions are power functions?

$\begin{array}{ccc}\hfill f\left(x\right)& =& 2x\cdot 4{x}^{3}\hfill \\ \hfill g\left(x\right)& =& -{x}^{5}+5{x}^{3}\hfill \\ \hfill h\left(x\right)& =& \frac{2{x}^{5}-1}{3{x}^{2}+4}\hfill \end{array}$

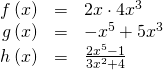
[reveal-answer q="fs-id1165134312227″]Show Solution[/reveal-answer]
[hidden-respond a="fs-id1165134312227″]

$f\left(x\right)\,$
is a power function because it tin exist written as $\,f\left(x\right)=8{x}^{5}.\,$
The other functions are non power functions.

[/subconscious-answer]

Identifying Stop Beliefs of Power Functions

(Figure) shows the graphs of $\,f\left(x\right)={x}^{2},\,g\left(x\right)={x}^{4}\,$ and $\,h\left(x\right)={x}^{6},\,$ which are all ability functions with even, whole-number powers. Notice that these graphs have similar shapes, very much like that of the quadratic function in the toolkit. However, every bit the ability increases, the graphs flatten somewhat nearly the origin and become steeper abroad from the origin.

Graph of three functions, h(x)=x^2 in green, g(x)=x^4 in orange, and f(x)=x^6 in blue. — **Effigy 2.** Even-power functions

To describe the behavior every bit numbers go larger and larger, we utilize the idea of infinity. We employ the symbol $\,\infty \,$ for positive infinity and $\,\mathrm{-\infty }\,$ for negative infinity. When nosotros say that " $x\,$ approaches infinity," which tin can be symbolically written as $\,x\to \infty ,\,$ nosotros are describing a behavior; we are saying that $\,x\,$ is increasing without bound.

With the positive fifty-fifty-ability function, every bit the input increases or decreases without bound, the output values become very large, positive numbers. Equivalently, we could draw this behavior by saying that as $\,x\,$ approaches positive or negative infinity, the $\,f\left(x\right)\,$ values increase without bound. In symbolic form, we could write

$\text{as }x\to ±\infty , f\left(x\right)\to \infty$

(Figure) shows the graphs of $\,f\left(x\right)={x}^{3},\,g\left(x\right)={x}^{5},$ and $\,h\left(x\right)={x}^{7},$ which are all power functions with odd, whole-number powers. Notice that these graphs look similar to the cubic function in the toolkit. Again, as the power increases, the graphs flatten virtually the origin and become steeper away from the origin.

Graph of three functions, f(x)=x^3 in green, g(x)=x^5 in orange, and h(x)=x^7 in blue. — **Effigy 3.** Odd-power functions

These examples illustrate that functions of the grade $\,f\left(x\right)={x}^{n}\,$ reveal symmetry of one kind or some other. First, in (Figure) we run into that even functions of the form $\,f\left(x\right)={x}^{n}\text{, }n\,$ even, are symmetric nearly the $\,y\text{-}$ axis. In (Figure) we see that odd functions of the course $\,f\left(x\right)={x}^{n}\text{, }n\,$ odd, are symmetric about the origin.

For these odd power functions, as $\,x\,$ approaches negative infinity, $\,f\left(x\right)\,$ decreases without spring. Every bit $\,x\,$ approaches positive infinity, $\,f\left(x\right)\,$ increases without bound. In symbolic class we write

$\begin{array}{l}\text{as} x\to -\infty , f\left(x\right)\to -\infty \\ \text{as} x\to \infty , f\left(x\right)\to \infty \end{array}$

The behavior of the graph of a function as the input values become very small ( $\,x\to -\infty \,$ ) and go very large ( $\,x\to \infty \,$ ) is referred to equally the end behavior of the office. We tin use words or symbols to describe finish behavior.

(Figure) shows the end behavior of power functions in the class $\,f\left(x\right)=k{x}^{n}\,$ where $\,n\,$ is a non-negative integer depending on the ability and the constant.

Graph of an even-powered function with a positive constant. As x goes to negative infinity, the function goes to positive infinity; as x goes to positive infinity, the function goes to positive infinity. Graph of an odd-powered function with a positive constant. As x goes to negative infinity, the function goes to positive infinity; as x goes to positive infinity, the function goes to negative infinity. Graph of an even-powered function with a negative constant. As x goes to negative infinity, the function goes to negative infinity; as x goes to positive infinity, the function goes to negative infinity. Graph of an odd-powered function with a negative constant. As x goes to negative infinity, the function goes to negative infinity; as x goes to positive infinity, the function goes to negative infinity. — **Figure 4.**

How To

Given a ability office $\,f\left(x\right)=k{x}^{n}\,$ where $\,n\,$ is a non-negative integer, place the terminate behavior.

Make up one's mind whether the power is even or odd.
Make up one's mind whether the abiding is positive or negative.
Use (Effigy) to place the end behavior.

Identifying the Terminate Beliefs of a Power Part

Describe the end behavior of the graph of $\,f\left(x\right)={x}^{8}.$

[reveal-reply q="fs-id1165135169237″]Testify Solution[/reveal-answer]
[hidden-respond a="fs-id1165135169237″]

The coefficient is 1 (positive) and the exponent of the power function is 8 (an even number). Every bit $\,x\,$ approaches infinity, the output (value of $\,f\left(x\right)\,$ ) increases without bound. Nosotros write equally $\,x\to \infty ,f\left(x\right)\to \infty .\,$ Every bit $\,x\,$ approaches negative infinity, the output increases without bound. In symbolic form, as $x\to -\infty , f\left(x\right)\to \infty .$ We can graphically represent the function as shown in (Effigy).

[/hidden-answer]

Identifying the End Behavior of a Power Function.

Depict the end behavior of the graph of $\,f\left(x\right)=-{x}^{9}.$

[reveal-answer q="fs-id1165137722696″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1165137722696″]

The exponent of the power role is 9 (an odd number). Because the coefficient is $\,-1\,$ (negative), the graph is the reflection nigh the $\,x\text{-}$ axis of the graph of $\,f\left(x\right)={x}^{9}.\,$ (Figure) shows that equally $\,x\,$ approaches infinity, the output decreases without bound. As $\,x\,$ approaches negative infinity, the output increases without bound. In symbolic form, nosotros would write

$\begin{array}{l}\text{as} x\to -\infty , f\left(x\right)\to \infty \\ \text{as} x\to \infty , f\left(x\right)\to -\infty \end{array}$

[/hidden-respond]

Assay

We can bank check our work by using the table feature on a graphing utility.

$x$	$f\left(x\right)$
–x	1,000,000,000
–v	i,953,125
0	0
5	–1,953,125
10	–i,000,000,000

We can see from (Figure) that, when nosotros substitute very small values for $\,x,\,$ the output is very large, and when we substitute very large values for $\,x,\,$ the output is very small (meaning that it is a very large negative value).

Endeavour It

Draw in words and symbols the cease beliefs of $\,f\left(x\right)=-5{x}^{4}.$

[reveal-answer q="fs-id1165137647550″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1165137647550″]

As $\,x\,$ approaches positive or negative infinity, $\,f\left(x\right)\,$ decreases without bound: as $\,x\to ±\infty , f\left(x\right)\to -\infty \,$ because of the negative coefficient.

[/hidden-answer]

Identifying Polynomial Functions

An oil pipeline bursts in the Gulf of Mexico, causing an oil slick in a roughly round shape. The slick is currently 24 miles in radius, merely that radius is increasing past eight miles each calendar week. We want to write a formula for the area covered past the oil slick by combining two functions. The radius $\,r\,$
of the spill depends on the number of weeks $\,w\,$
that accept passed. This relationship is linear.

$r\left(w\right)=24+8w$

Nosotros can combine this with the formula for the area $\,A\,$
of a circle.

$A\left(r\right)=\pi {r}^{2}$

Composing these functions gives a formula for the area in terms of weeks.

$\begin{array}{ccc}\hfill A\left(w\right)& =& A\left(r\left(w\right)\right)\hfill \\ & =& A\left(24+8w\right)\hfill \\ & =& \pi {\left(24+8w\right)}^{2}\hfill \end{array}$

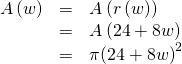
Multiplying gives the formula.

$A\left(w\right)=576\pi +384\pi w+64\pi {w}^{2}$

This formula is an example of a polynomial function. A polynomial function consists of either zero or the sum of a finite number of not-zero terms, each of which is a product of a number, chosen the coefficient of the term, and a variable raised to a non-negative integer power.

Polynomial Functions

Let $\,n\,$
be a non-negative integer. A polynomial function is a function that tin can be written in the grade

$f\left(x\right)={a}_{n}{x}^{n}+...+{a}_{2}{x}^{2}+{a}_{1}x+{a}_{0}$

This is chosen the full general form of a polynomial part. Each $\,{a}_{i}\,$
is a coefficient and can exist whatever real number, but
$\,{a}_{n}\,$ cannot = 0. Each expression $\,{a}_{i}{x}^{i}\,$
is a term of a polynomial function.

Identifying Polynomial Functions

Which of the following are polynomial functions?

$\begin{array}{ccc}\hfill f\left(x\right)& =& 2{x}^{3}\cdot 3x+4\hfill \\ \hfill g\left(x\right)& =& -x\left({x}^{2}-4\right)\hfill \\ \hfill h\left(x\right)& =& 5\sqrt{x+2}\hfill \end{array}$

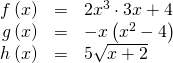
[reveal-answer q="fs-id1165134221783″]Show Solution[/reveal-answer]
[subconscious-answer a="fs-id1165134221783″]

The start two functions are examples of polynomial functions because they tin be written in the class $\,f\left(x\right)={a}_{n}{x}^{n}+...+{a}_{2}{x}^{2}+{a}_{1}x+{a}_{0},\,$
where the powers are non-negative integers and the coefficients are real numbers.

[/hidden-answer]

Identifying the Degree and Leading Coefficient of a Polynomial Function

Because of the class of a polynomial office, we can see an space diversity in the number of terms and the power of the variable. Although the order of the terms in the polynomial part is not of import for performing operations, we typically arrange the terms in descending order of power, or in general grade. The degree of the polynomial is the highest ability of the variable that occurs in the polynomial; information technology is the power of the first variable if the part is in general grade. The leading term is the term containing the highest power of the variable, or the term with the highest caste. The leading coefficient is the coefficient of the leading term.

Terminology of Polynomial Functions

We oft rearrange polynomials then that the powers are descending.

Diagram to show what the components of the leading term in a function are. The leading coefficient is a_n and the degree of the variable is the exponent in x^n. Both the leading coefficient and highest degree variable make up the leading term. So the function looks like f(x)=a_nx^n +…+a_2x^2+a_1x+a_0.

When a polynomial is written in this fashion, we say that it is in general form.

How To

Given a polynomial function, identify the degree and leading coefficient.

Find the highest power of $\,x\,$
to determine the caste function.
Identify the term containing the highest ability of $\,x\,$
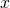
to find the leading term.
Identify the coefficient of the leading term.

Identifying the Degree and Leading Coefficient of a Polynomial Function

Place the caste, leading term, and leading coefficient of the following polynomial functions.

$\begin{array}{ccc}\hfill f\left(x\right)& =& 3+2{x}^{2}-4{x}^{3}\hfill \\ \hfill g\left(t\right)& =& 5{t}^{5}-2{t}^{3}+7t\hfill \\ h\left(p\right)\hfill & =& 6p-{p}^{3}-2\hfill \end{array}$

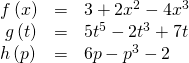
Identify the degree, leading term, and leading coefficient of the polynomial $\,f\left(x\right)=4{x}^{2}-{x}^{6}+2x-6.$

[reveal-answer q="fs-id1165135701674″]Evidence Solution[/reveal-answer]
[hidden-respond a="fs-id1165135701674″]

The degree is six. The leading term is $\,-{x}^{6}.\,$ The leading coefficient is $\,-1.$

[/hidden-answer]

Identifying End Beliefs of Polynomial Functions

Knowing the caste of a polynomial function is useful in helping us predict its end beliefs. To determine its cease behavior, look at the leading term of the polynomial function. Because the ability of the leading term is the highest, that term will grow significantly faster than the other terms as $\,x\,$ gets very large or very modest, so its behavior will dominate the graph. For any polynomial, the end behavior of the polynomial will friction match the end beliefs of the power function consisting of the leading term. See (Effigy).

Polynomial Role	Leading Term	Graph of Polynomial Role
$f\left(x\right)=5{x}^{4}+2{x}^{3}-x-4$	$5{x}^{4}$
$f\left(x\right)=-2{x}^{6}-{x}^{5}+3{x}^{4}+{x}^{3}$	$-2{x}^{6}$
$f\left(x\right)=3{x}^{5}-4{x}^{4}+2{x}^{2}+1$	$3{x}^{5}$
$f\left(x\right)=-6{x}^{3}+7{x}^{2}+3x+1$	$-6{x}^{3}$

Identifying End Behavior and Caste of a Polynomial Function

Describe the end behavior and determine a possible degree of the polynomial function in (Effigy).

Graph of an odd-degree polynomial. — **Figure 7.**

[reveal-respond q="fs-id1165135251309″]Bear witness Solution[/reveal-respond]
[subconscious-answer a="fs-id1165135251309″]

Every bit the input values $\,x\,$
get very large, the output values $\,f\left(x\right)\,$ increment without bound. Equally the input values $\,x\,$
become very small, the output values $\,f\left(x\right)\,$ decrease without bound. We tin describe the end beliefs symbolically by writing

$\begin{array}{l}\text{as} x\to -\infty , f\left(x\right)\to -\infty \\ \text{as} x\to \infty , f\left(x\right)\to \infty \end{array}$

In words, we could say that as $\,x\,$ values arroyo infinity, the function values approach infinity, and as $\,x\,$ values arroyo negative infinity, the function values approach negative infinity.

We can tell this graph has the shape of an odd caste power function that has not been reflected, so the degree of the polynomial creating this graph must exist odd and the leading coefficient must be positive.

[/hidden-answer]

Try It

Depict the end beliefs, and determine a possible degree of the polynomial office in (Figure).

Graph of an even-degree polynomial. — **Effigy 8.**

[reveal-reply q="fs-id1165134047710″]Evidence Solution[/reveal-answer]
[hidden-respond a="fs-id1165134047710″]

As $\,x\to \infty , f\left(x\right)\to -\infty ; as x\to -\infty , f\left(x\right)\to -\infty .\,$ Information technology has the shape of an even degree power office with a negative coefficient.

[/hidden-answer]

Identifying End Behavior and Caste of a Polynomial Function

Given the function $\,f\left(x\right)=-3{x}^{2}\left(x-1\right)\left(x+4\right),\,$ express the function as a polynomial in full general form, and determine the leading term, degree, and end behavior of the function.

[reveal-answer q="fs-id1165137401107″]Evidence Solution[/reveal-answer]
[hidden-reply a="fs-id1165137401107″]

Obtain the full general course by expanding the given expression for $\,f\left(x\right).$

$\begin{array}{ccc}\hfill f\left(x\right)& =& -3{x}^{2}\left(x-1\right)\left(x+4\right)\hfill \\ & =& -3{x}^{2}\left({x}^{2}+3x-4\right)\hfill \\ & =& -3{x}^{4}-9{x}^{3}+12{x}^{2}\hfill \end{array}$

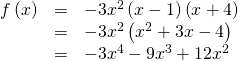
The general grade is $\,f\left(x\right)=-3{x}^{4}-9{x}^{3}+12{x}^{2}.\,$
The leading term is $\,-3{x}^{4};\,$
therefore, the caste of the polynomial is 4. The degree is fifty-fifty (4) and the leading coefficient is negative (–3), then the end behavior is

$\begin{array}{l}\text{as} x\to -\infty , f\left(x\right)\to -\infty \\ \text{as} x\to \infty , f\left(x\right)\to -\infty \end{array}$ [/hidden-answer]

Try Information technology

Given the office $\,f\left(x\right)=0.2\left(x-2\right)\left(x+1\right)\left(x-5\right),\,$ express the function as a polynomial in general form and decide the leading term, degree, and end beliefs of the function.

[reveal-reply q="fs-id1165135409431″]Show Solution[/reveal-answer]
[hidden-respond a="fs-id1165135409431″]

The leading term is $\,0.2{x}^{3},\,$ so it is a degree 3 polynomial. As $\,x\,$ approaches positive infinity, $\,f\left(x\right)\,$ increases without leap; equally $\,x\,$ approaches negative infinity, $\,f\left(x\right)\,$ decreases without bound.

[/subconscious-reply]

Identifying Local Behavior of Polynomial Functions

In addition to the end beliefs of polynomial functions, we are also interested in what happens in the "centre" of the function. In particular, we are interested in locations where graph beliefs changes. A turning point is a point at which the role values modify from increasing to decreasing or decreasing to increasing.

We are also interested in the intercepts. As with all functions, the y-intercept is the point at which the graph intersects the vertical axis. The point corresponds to the coordinate pair in which the input value is zero. Considering a polynomial is a function, only one output value corresponds to each input value and then there can exist only i y-intercept $\,\left(0,{a}_{0}\right).\,$ The ten-intercepts occur at the input values that represent to an output value of null. It is possible to have more one ten-intercept. Come across (Figure).

Intercepts and Turning Points of Polynomial Functions

A turning point of a graph is a bespeak at which the graph changes management from increasing to decreasing or decreasing to increasing. The y-intercept is the point at which the function has an input value of zip. The x-intercepts are the points at which the output value is zero.

How To

Given a polynomial function, make up one's mind the intercepts.

Make up one's mind the y-intercept past setting 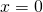$\,x=0\,$ and finding the corresponding output value.
Determine the 10-intercepts by solving for the input values that yield an output value of zero.

Determining the Intercepts of a Polynomial Function

Given the polynomial function $\,f\left(x\right)=\left(x-2\right)\left(x+1\right)\left(x-4\right),\,$ written in factored form for your convenience, determine the y– and ten-intercepts.

[reveal-reply q="fs-id1165135251466″]Show Solution[/reveal-answer]
[subconscious-respond a="fs-id1165135251466″]

The y-intercept occurs when the input is zippo so substitute 0 for $\,x.$

$\begin{array}{ccc}\hfill f\left(0\right)& =& {\left(0\right)}^{4}-4{\left(0\right)}^{2}-45\hfill \\ & =& -45\hfill \end{array}$

The y-intercept is (0, 8).

The x-intercepts occur when the output is nothing.

$0=\left(x-2\right)\left(x+1\right)\left(x-4\right)$

$\begin{array}{ccccccccccc}\hfill x-2& =& 0\hfill & \phantom{\rule{2em}{0ex}}\text{or}\phantom{\rule{2em}{0ex}}& \hfill x+1& =& 0\hfill & \phantom{\rule{2em}{0ex}}\text{or}\phantom{\rule{2em}{0ex}}& \hfill x-4& =& 0\hfill \\ \hfill x& =& 2\hfill & \phantom{\rule{2em}{0ex}}\text{or}\phantom{\rule{2em}{0ex}}& \hfill x& =& -1\hfill & \phantom{\rule{2em}{0ex}}\text{or}\phantom{\rule{2em}{0ex}}& \hfill x& =& 4\hfill \end{array}$

The x-intercepts are $\,\left(2,0\right),\left(-1,0\right),\,$ and $\,\left(4,0\right).$

We tin can see these intercepts on the graph of the role shown in (Figure).

Graph of f(x)=(x-2)(x+1)(x-4), which labels all the intercepts. — **Figure 10.**

[/hidden-answer]

Determining the Intercepts of a Polynomial Part with Factoring

Given the polynomial function $\,f\left(x\right)={x}^{4}-4{x}^{2}-45,\,$ determine the y– and ten-intercepts.

[reveal-reply q="fs-id1165137634473″]Show Solution[/reveal-reply]
[hidden-answer a="fs-id1165137634473″]

The y-intercept occurs when the input is zero.

$\begin{array}{ccc}\hfill f\left(0\right)& =& {\left(0\right)}^{4}-4{\left(0\right)}^{2}-45\hfill \\ & =& -45\hfill \end{array}$

The y-intercept is $\,\left(0,-45\right).$

The x-intercepts occur when the output is zero. To determine when the output is zero, we will need to factor the polynomial.

$\begin{array}{ccc}\hfill f\left(x\right)& =& {x}^{4}-4{x}^{2}-45\hfill \\ & =& \left({x}^{2}-9\right)\left({x}^{2}+5\right)\hfill \\ & =& \left(x-3\right)\left(x+3\right)\left({x}^{2}+5\right)\hfill \end{array}$
$\phantom{\rule{2em}{0ex}}0=\left(x-3\right)\left(x+3\right)\left({x}^{2}+5\right)$

$\begin{array}{ccccccccc}\hfill x-3& =& 0\hfill & \text{or}& \hfill x+3& =& 0\hfill &\text{or}& {x}^{2}+5=0\\ \hfill x& =& 3\hfill & \text{or} & \hfill x& =& -3\hfill & \text{or}& (\text{no real solution)}\end{array}$

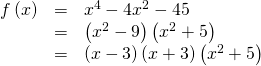
The ten-intercepts are $\,\left(3,0\right)\,$ and $\,\left(-3,0\right).$

We can see these intercepts on the graph of the role shown in (Figure). Nosotros tin see that the role is even because $\,f\left(x\right)=f\left(-x\right).$

Graph of f(x)=x^4-4x^2-45, which labels all the intercepts at (-3, 0), (3, 0), and (0, -45). — **Figure xi.**

[/subconscious-reply]

Try Information technology

Given the polynomial function $\,f\left(x\right)=2{x}^{3}-6{x}^{2}-20x,\,$ decide the y– and 10-intercepts.

[reveal-answer q="fs-id1165137762370″]Testify Solution[/reveal-answer]
[subconscious-answer a="fs-id1165137762370″]

y-intercept $\,\left(0,0\right);\,$ 10-intercepts $\,\left(0,0\right),\left(-2,0\right),\,$ and $\left(5,0\right)$

[/subconscious-respond]

Comparing Smooth and Continuous Graphs

The degree of a polynomial office helps united states of america to make up one's mind the number of ten-intercepts and the number of turning points. A polynomial role of $\,n\text{th}\,$ degree is the product of $\,n\,$ factors, and then information technology will have at most $\,n\,$ roots or zeros, or x-intercepts. The graph of the polynomial function of caste $\,n\,$ must have at nearly $\,n-1\,$ turning points. This means the graph has at most one fewer turning point than the degree of the polynomial or 1 fewer than the number of factors.

A continuous function has no breaks in its graph: the graph can be drawn without lifting the pen from the paper. A smooth curve is a graph that has no sharp corners. The turning points of a smooth graph must e'er occur at rounded curves. The graphs of polynomial functions are both continuous and smooth.

Determining the Number of Intercepts and Turning Points of a Polynomial

Without graphing the function, make up one's mind the local behavior of the function by finding the maximum number of x-intercepts and turning points for $\,f\left(x\right)=-3{x}^{10}+4{x}^{7}-{x}^{4}+2{x}^{3}.$

[reveal-reply q="fs-id1165135414339″]Show Solution[/reveal-respond]
[hidden-answer a="fs-id1165135414339″]

The polynomial has a degree of $\,10,\,$ so there are at most ten x-intercepts and at most ix turning points.

[/hidden-answer]

Endeavor It

Without graphing the function, determine the maximum number of x-intercepts and turning points for $\,f\left(x\right)=108-13{x}^{9}-8{x}^{4}+14{x}^{12}+2{x}^{3}.$

[reveal-respond q="fs-id1165137660801″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1165137660801″]

There are at virtually 12 $\,x\text{-}$ intercepts and at most 11 turning points.

[/hidden-respond]

Drawing Conclusions almost a Polynomial Function from the Graph

What can we conclude about the polynomial represented by the graph shown in (Figure) based on its intercepts and turning points?

[reveal-answer q="fs-id1165137737264″]Show Solution[/reveal-reply]
[subconscious-answer a="fs-id1165137737264″]

The finish beliefs of the graph tells us this is the graph of an even-degree polynomial. Encounter (Figure).

Graph of an even-degree polynomial that denotes the turning points and intercepts. — **Figure 13.**

The graph has 2 10-intercepts, suggesting a caste of 2 or greater, and 3 turning points, suggesting a degree of four or greater. Based on this, it would be reasonable to conclude that the degree is even and at least 4.[/hidden-answer]

Try Information technology

What can nosotros conclude about the polynomial represented past the graph shown in (Figure) based on its intercepts and turning points?

[reveal-answer q="fs-id1165137666790″]Evidence Solution[/reveal-answer]
[hidden-answer a="fs-id1165137666790″]

The end behavior indicates an odd-degree polynomial office; there are 3 $\,x\text{-}$ intercepts and 2 turning points, so the caste is odd and at to the lowest degree iii. Considering of the end beliefs, nosotros know that the lead coefficient must be negative.

[/subconscious-answer]

Cartoon Conclusions about a Polynomial Office from the Factors

Given the function $\,f\left(x\right)=-4x\left(x+3\right)\left(x-4\right),\,$
determine the local behavior.

[reveal-answer q="fs-id1165135457721″]Bear witness Solution[/reveal-answer]
[subconscious-answer a="fs-id1165135457721″]

The y-intercept is found by evaluating $\,f\left(0\right).$

$\begin{array}{ccc}\hfill f\left(0\right)& =& -4\left(0\right)\left(0+3\right)\left(0-4\\ & =& 0\hfill \end{array}$

The y-intercept is $\,\left(0,0\right).$

The ten-intercepts are found past determining the zeros of the part.

$0=-4x\left(x+3\right)\left(x-4\right)$

$\begin{array}{ccccccccccc}\hfill x& =& 0\hfill & \phantom{\rule{2em}{0ex}}\text{or}\phantom{\rule{2em}{0ex}}& \hfill x+3& =& 0\hfill & \phantom{\rule{2em}{0ex}}\text{or}\phantom{\rule{2em}{0ex}}& \hfill x-4& =& 0\hfill \\ x& =& 0& \phantom{\rule{2em}{0ex}}\text{or}\phantom{\rule{2em}{0ex}}& x& =& -3& \phantom{\rule{2em}{0ex}}\text{or}\phantom{\rule{2em}{0ex}}& x& =& 4\end{array}$

The ten-intercepts are $\,\left(0,0\right),\left(-3,0\right),\,$ and $\,\left(4,0\right).$

The caste is 3 so the graph has at almost ii turning points.

[/hidden-respond]

Try It

Given the function $\,f\left(x\right)=0.2\left(x-2\right)\left(x+1\right)\left(x-5\right),\,$ determine the local beliefs.

[reveal-answer q="fs-id1165137833005″]Evidence Solution[/reveal-answer]
[hidden-reply a="fs-id1165137833005″]

The $\,x\text{-}$ intercepts are $\,\left(2,0\right),\left(-1,0\right),$ and $\,\left(5,0\right),\,$ the y-intercept is $\,\left(0,\text{2}\right),\,$ and the graph has at almost 2 turning points.

[/subconscious-answer]

Central Equations

full general form of a polynomial role

$f\left(x\right)={a}_{n}{x}^{n}+...+{a}_{2}{x}^{2}+{a}_{1}x+{a}_{0}$

Cardinal Concepts

Section Exercises

Exact

Explain the deviation between the coefficient of a ability function and its degree.

[reveal-answer q="fs-id1165137423709″]Show Solution[/reveal-reply]
[hidden-answer a="fs-id1165137423709″]

The coefficient of the power role is the real number that is multiplied past the variable raised to a power. The degree is the highest ability appearing in the function.

[/hidden-answer]

If a polynomial function is in factored course, what would be a good kickoff footstep in guild to determine the degree of the part?

In general, explicate the finish behavior of a power role with odd degree if the leading coefficient is positive.

[reveal-answer q="fs-id1165135205853″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1165135205853″]

As $\,x\,$
decreases without bound, and then does $\,f\left(x\right).\,$
As $\,x\,$
increases without spring, then does $\,f\left(x\right).$

[/hidden-answer]

What is the relationship between the degree of a polynomial function and the maximum number of turning points in its graph?

What can we conclude if, in full general, the graph of a polynomial function exhibits the following end behavior? As $\,x\to -\infty ,\,f\left(x\right)\to -\infty \,$
and as $\,x\to \infty ,\,f\left(x\right)\to -\infty .\,$

[reveal-answer q="fs-id1165137679007″]Show Solution[/reveal-answer]
[hidden-reply a="fs-id1165137679007″]

The polynomial function is of fifty-fifty degree and leading coefficient is negative.

[/subconscious-reply]

Algebraic

For the following exercises, place the part as a power function, a polynomial part, or neither.

$f\left(x\right)={x}^{5}$

$f\left(x\right)={\left({x}^{2}\right)}^{3}$

[reveal-answer q="fs-id1165134043753″]Show Solution[/reveal-answer]
[subconscious-answer a="fs-id1165134043753″]

Power office

[/hidden-reply]

$f\left(x\right)=x-{x}^{4}$

$f\left(x\right)=\frac{{x}^{2}}{{x}^{2}-1}$

[reveal-answer q="fs-id1165137723151″]Evidence Solution[/reveal-answer]
[hidden-answer a="fs-id1165137723151″]

Neither

[/hidden-reply]

$f\left(x\right)=2x\left(x+2\right){\left(x-1\right)}^{2}$

$f\left(x\right)={3}^{x+1}$

[reveal-answer q="fs-id1165137619578″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1165137619578″]

Neither

[/subconscious-answer]

For the following exercises, find the caste and leading coefficient for the given polynomial.

$-3x{}^{4}$

$7-2{x}^{2}$

[reveal-answer q="fs-id1165137424474″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1165137424474″]

Degree = 2, Coefficient = –2

[/subconscious-answer]

$-2{x}^{2}-3{x}^{5}+x-6$

$x\left(4-{x}^{2}\right)\left(2x+1\right)$

[reveal-reply q="fs-id1165137842483″]Prove Solution[/reveal-answer]
[hidden-answer a="fs-id1165137842483″]

Degree =four, Coefficient = –two

[/hidden-respond]

${x}^{2}{\left(2x-3\right)}^{2}$

For the post-obit exercises, determine the end behavior of the functions.

$f\left(x\right)={x}^{4}$

[reveal-respond q="fs-id1165137445856″]Show Solution[/reveal-respond]
[hidden-answer a="fs-id1165137445856″]

$\text{As}\,x\to \infty ,\,\,f\left(x\right)\to \infty ,\,\text{as}\,x\to -\infty ,\,f\left(x\right)\to \infty$

[/subconscious-answer]

$f\left(x\right)={x}^{3}$

$f\left(x\right)=-{x}^{4}$

[reveal-answer q="fs-id1165137643430″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1165137643430″]

$\text{As}\,x\to -\infty ,\,\,f\left(x\right)\to -\infty ,\,\text{as}\,x\to \infty ,\,f\left(x\right)\to -\infty$

[/hidden-answer]

$f\left(x\right)=-{x}^{9}$

$f\left(x\right)=-2{x}^{4}-3{x}^{2}+x-1$

[reveal-answer q="fs-id1165137656888″]Show Solution[/reveal-respond]
[subconscious-respond a="fs-id1165137656888″]

$\text{As}\,x\to -\infty ,\,\,f\left(x\right)\to -\infty ,\,\text{as}\,x\to \infty ,\,f\left(x\right)\to -\infty$

[/hidden-answer]

$f\left(x\right)=3{x}^{2}+x-2$

$f\left(x\right)={x}^{2}\left(2{x}^{3}-x+1\right)$

[reveal-respond q="fs-id1165137794123″]Bear witness Solution[/reveal-reply]
[hidden-respond a="fs-id1165137794123″]

$\text{As}\,x\to \infty ,\,\,f\left(x\right)\to \infty ,\,\text{as}\,x\to -\infty ,\,f\left(x\right)\to -\infty$

[/hidden-answer]

$f\left(x\right)={\left(2-x\right)}^{7}$

For the following exercises, discover the intercepts of the functions.

$f\left(t\right)=2\left(t-1\right)\left(t+2\right)\left(t-3\right)$

[reveal-reply q="fs-id1165135697918″]Bear witness Solution[/reveal-answer]
[hidden-reply a="fs-id1165135697918″]

y-intercept is $\,\left(0,12\right),\,$ t-intercepts are $\,\left(1,0\right);\left(-2,0\right);\text{and }\left(3,0\right).$

[/hidden-answer]

$g\left(n\right)=-2\left(3n-1\right)\left(2n+1\right)$

$f\left(x\right)={x}^{4}-16$

[reveal-answer q="fs-id1165137728286″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1165137728286″]

y-intercept is $\,\left(0,-16\right).\,$ 10-intercepts are $\,\left(2,0\right)\,$ and $\,\left(-2,0\right).$

[/subconscious-answer]

$f\left(x\right)={x}^{3}+27$

$f\left(x\right)=x\left({x}^{2}-2x-8\right)$

[reveal-answer q="fs-id1165137896961″]Show Solution[/reveal-answer]
[subconscious-answer a="fs-id1165137896961″]

y-intercept is $\,\left(0,0\right).\,$ x-intercepts are $\,\left(0,0\right),\left(4,0\right),\,$ and $\,\left(-2, 0\right).$

[/hidden-answer]

$f\left(x\right)=\left(x+3\right)\left(4{x}^{2}-1\right)$

Graphical

For the following exercises, determine the least possible degree of the polynomial function shown.

Graph of an odd-degree polynomial.

[reveal-reply q="fs-id1165135388469″]Show Solution[/reveal-answer]
[hidden-reply a="fs-id1165135388469″]

[/hidden-reply]

Graph of an even-degree polynomial.

Graph of an odd-degree polynomial.

[reveal-respond q="fs-id1165135181683″]Evidence Solution[/reveal-answer]
[hidden-answer a="fs-id1165135181683″]

[/hidden-respond]

Graph of an odd-degree polynomial.

[reveal-reply q="fs-id1165135255943″]Prove Solution[/reveal-answer]
[hidden-reply a="fs-id1165135255943″]

[/hidden-reply]

Graph of an even-degree polynomial.

Graph of an odd-degree polynomial.

[reveal-reply q="fs-id1165135191388″]Show Solution[/reveal-answer]
[hidden-respond a="fs-id1165135191388″]

[/hidden-respond]

Graph of an even-degree polynomial.

For the following exercises, determine whether the graph of the function provided is a graph of a polynomial role. If and then, determine the number of turning points and the least possible caste for the function.

Graph of an odd-degree polynomial.

[reveal-answer q="fs-id1165137444866″]Prove Solution[/reveal-answer]
[hidden-answer a="fs-id1165137444866″]

Yes. Number of turning points is ii. To the lowest degree possible degree is 3.

[/hidden-answer]

Graph of an equation.

Graph of an even-degree polynomial.

[reveal-respond q="fs-id1165137570516″]Testify Solution[/reveal-answer]
[hidden-answer a="fs-id1165137570516″]

Yes. Number of turning points is 1. Least possible degree is two.

[/hidden-reply]

Graph of an odd-degree polynomial.

[reveal-answer q="fs-id1165134042451″]Show Solution[/reveal-answer]
[subconscious-answer a="fs-id1165134042451″]

Yes. Number of turning points is 0. Least possible degree is one.

[/subconscious-respond]

Graph of an equation.

[reveal-answer q="fs-id1165133310452″]Show Solution[/reveal-answer]
[hidden-reply a="fs-id1165133310452″]

No.

[/hidden-answer]

Graph of an odd-degree polynomial.

[reveal-answer q="fs-id1165137569703″]Show Solution[/reveal-answer]
[hidden-reply a="fs-id1165137569703″]

Yes. Number of turning points is 0. Least possible caste is 1.

[/hidden-answer]

Numeric

For the post-obit exercises, make a table to confirm the cease beliefs of the office.

$f\left(x\right)=-{x}^{3}$

$f\left(x\right)={x}^{4}-5{x}^{2}$

[reveal-answer q="983153″]Testify Solution[/reveal-answer]
[subconscious-reply a="983153″]


$x$	$f\left(x\right)$
10	9,500
100	99,950,000
–10	9,500
–100	99,950,000

$\text{as}\,x\to -\infty ,\,\,f\left(x\right)\to \infty ,\,\text{as}\,x\to \infty ,\,f\left(x\right)\to \infty$

[/hidden-reply]

$f\left(x\right)={x}^{2}{\left(1-x\right)}^{2}$

$f\left(x\right)=\left(x-1\right)\left(x-2\right)\left(3-x\right)$

[reveal-respond q="fs-id1165134122928″]Show Solution[/reveal-answer]
[subconscious-answer a="fs-id1165134122928″]


$x$	$f\left(x\right)$
10	–504
100	–941,094
–x	1,716
–100	1,061,106

$\text{as}\,x\to -\infty ,\,\,f\left(x\right)\to \infty ,\,\text{as}\,x\to \infty ,\,f\left(x\right)\to -\infty$

[/subconscious-respond]

$f\left(x\right)=\frac{{x}^{5}}{10}-{x}^{4}$

Technology

For the following exercises, graph the polynomial functions using a calculator. Based on the graph, determine the intercepts and the end behavior.

$f\left(x\right)={x}^{3}\left(x-2\right)$

[reveal-answer q="41150″]Testify Solution[/reveal-answer]
[hidden-answer a="41150″]

Graph of f(x)=x^3(x-2).

The $\,y\text{-}$ intercept is $\,\left(0, 0\right).\,$
The $\,x\text{-}$ intercepts are $\,\left(0, 0\right),\text{ }\left(2, 0\right).\,$
$\text{As}\,x\to -\infty ,\,\,f\left(x\right)\to \infty ,\,\text{as}\,x\to \infty ,\,f\left(x\right)\to \infty$

[/subconscious-answer]

$f\left(x\right)=x\left(x-3\right)\left(x+3\right)$

$f\left(x\right)=x\left(14-2x\right)\left(10-2x\right)$

[reveal-answer q="891902″]Show Solution[/reveal-answer]
[hidden-answer a="891902″]

Graph of f(x)=x(14-2x)(10-2x).

The $\,y\text{-}$ intercept is $\,\left(0,0\right)$
. The $\,x\text{-}$ intercepts are $\,\left(0, 0\right),\text{ }\left(5, 0\right),\text{ }\left(7, 0\right).\,$
$\text{As}\,x\to -\infty ,\,\,f\left(x\right)\to -\infty ,\,\text{as}\,x\to \infty ,\,f\left(x\right)\to \infty$

[/hidden-respond]

$f\left(x\right)=x\left(14-2x\right){\left(10-2x\right)}^{2}$

$f\left(x\right)={x}^{3}-16x$

[reveal-reply q="218879″]Prove Solution[/reveal-answer]
[subconscious-respond a="218879″]

The $\,y\text{-}$ intercept is $\,\left(0, 0\right).\,$ The $\,x\text{-}$ intercept is $\,\left(-4, 0\right),\text{ }\left(0, 0\right),\text{ }\left(4, 0\right).\,$
$As\,x\to -\infty ,\,\,f\left(x\right)\to -\infty ,\,\text{as}\,x\to \infty ,\,f\left(x\right)\to \infty$

[/subconscious-respond]

$f\left(x\right)={x}^{3}-27$

$f\left(x\right)={x}^{4}-81$

[reveal-answer q="110405″]Testify Solution[/reveal-answer]
[hidden-answer a="110405″]

Graph of f(x)=x^3-27.

The $\,y\text{-}$ intercept is $\,\left(0, -81\right).\,$
The $\,x\text{-}$ intercept are $\,\left(3, 0\right),\text{ }\left(-3, 0\right).\,$
$\text{As}\,x\to -\infty ,\,\,f\left(x\right)\to \infty ,\,\text{as}\,x\to \infty ,\,f\left(x\right)\to \infty$

[/hidden-answer]

$f\left(x\right)=-{x}^{3}+{x}^{2}+2x$

$f\left(x\right)={x}^{3}-2{x}^{2}-15x$

[reveal-respond q="678775″]Prove Solution[/reveal-answer]
[subconscious-respond a="678775″]

Graph of f(x)=-x^3+x^2+2x. The $\,y\text{-}$ intercept is $\,\left(0, 0\right).\,$ The $\,x\text{-}$ intercepts are $\,\left(-3, 0\right),\text{ }\left(0, 0\right),\text{ }\left(5, 0\right).\,$
$\text{As}\,x\to -\infty ,\,\,f\left(x\right)\to -\infty ,\,\text{as}\,x\to \infty ,\,f\left(x\right)\to \infty$ [/hidden-answer]

$f\left(x\right)={x}^{3}-0.01x$

Extensions

For the following exercises, use the information nearly the graph of a polynomial office to determine the role. Presume the leading coefficient is 1 or –one. There may be more than than one correct answer.

[reveal-answer q="fs-id1165135160156″]Evidence Solution[/reveal-answer]
[hidden-answer a="fs-id1165135160156″]

$f\left(x\right)={x}^{2}-4$

[/subconscious-reply]

[reveal-answer q="fs-id1165134389974″]Evidence Solution[/reveal-answer]
[subconscious-reply a="fs-id1165134389974″]

$f\left(x\right)={x}^{3}-4{x}^{2}+4x$

[/hidden-reply]

The $\,y-$ intercept is $\,\left(0,1\right).\,$ There is no $\,x-$ intercept. Degree is 4.

End beliefs: $\,\text{as}\,x\to -\infty ,\,\,f\left(x\right)\to \infty ,\,\text{as}\,x\to \infty ,\,f\left(x\right)\to \infty .$

[reveal-respond q="fs-id1165137922537″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1165137922537″]

$f\left(x\right)={x}^{4}+1$

[/hidden-answer]

Real-World Applications

For the following exercises, use the written statements to construct a polynomial function that represents the required data.

An oil slick is expanding equally a circle. The radius of the circle is increasing at the rate of twenty meters per day. Limited the expanse of the circle as a function of $\,d,\,$ the number of days elapsed.

A cube has an edge of 3 feet. The edge is increasing at the rate of 2 feet per minute. Express the volume of the cube as a function of $\,m,\,$ the number of minutes elapsed.

[reveal-answer q="fs-id1165134032299″]Show Solution[/reveal-reply]
[hidden-respond a="fs-id1165134032299″]

$V\left(m\right)=8{m}^{3}+36{m}^{2}+54m+27$

[/subconscious-respond]

A rectangle has a length of ten inches and a width of half dozen inches. If the length is increased by $\,x\,$ inches and the width increased by twice that amount, express the area of the rectangle equally a function of $\,x.$

An open box is to exist constructed past cut out square corners of $\,x-$ inch sides from a piece of cardboard viii inches past viii inches and then folding up the sides. Limited the volume of the box as a function of $\,x.$

[reveal-answer q="fs-id1165135571779″]Bear witness Solution[/reveal-answer]
[hidden-answer a="fs-id1165135571779″]

$V\left(x\right)=4{x}^{3}-32{x}^{2}+64x$

[/subconscious-reply]

A rectangle is twice every bit long as it is wide. Squares of side two anxiety are cut out from each corner. Then the sides are folded upwards to make an open box. Express the volume of the box as a function of the width ( $x$ ).